Note Taux
ACE Taux :
analyse ACE de la performance des obligations et des points de courbe (constant maturity)
Rappelons le cahier des charges de ACE, qui doit produire tous les jours :
i) le Rendement de l’actif à conditions inchangées, ou Rendement ACE
ii) un Niveau de Valorisation, ce qui permet de découper l’indice Total Return en deux termes :
iii) l’indice Investment Return qui est le cumul de jour en jour du Rendement ACE
iv) l’indice Speculative Return qui suit les variations de Valorisation
ACE pour une obligation
ACE s’applique naturellement aux obligations avec l’aide du calcul actuariel. En définissant les « conditions de marché inchangées » par « son taux actuariel est inchangé », les réponses viennent toutes seules :
Question (ii) : Quel est son indicateur de Niveau ?
C’est le taux actuariel, comme on vient de le décider
Question (i) : Quel est son Rendement à conditions inchangées ?
C’est encore le taux actuariel, grâce à la propriété suivante :
la formule ① ci-dessous du calcul actuariel montre que si pendant un laps de temps, un actif commence et finit avec le même taux actuariel, sa performance annualisée est égale à ce taux.
Dans le cas général, la performance Total Return de l’obligation pendant le laps de temps \text { Δt } est connue par la variation du prix et le coupon s’il y en a un qui tombe à la fin. On peut aussi écrire grâce aux formules du calcul actuariel :
\text { Total Return pendant } \Delta t=\text { perfTR }=(1+Y)^{\Delta t}-1-\operatorname{sensi} * \Delta Y ①
Avec \text { Y } le taux actuariel, \text { ΔY } la variation de taux, et sensi la sensibilité aux taux.
Quand on passe d’un jour à l’autre, \Delta t=1 / 365 ou 3 / 365 est petit et on peut alors écrire
\text { Total Return pendant } \Delta t=\text { perfTR }=\log (1+Y)^{*} \Delta t-\operatorname{sensi}^{*}\Delta Y②
Remarques techniques
-/ Il est possible de bien construire la sensibilité avec la durée et le taux en fin de période, de sorte que la formule ① soit une égalité et non une approximation linéaire.
-/ Pour avoir la formule ②, e^{\log (1+Y)^{*} \Delta t}-1 a été assimilé à \log (1+Y) ^{*}\Delta t.
Avec un passage de week-end \Delta t=3 / 365 et Y<5 \% l’erreur d’approximation est inférieure au millième de \text { bp }\left(10^{-7}\right). Si on annualise l’approximation avec \Delta t=3 / 365 et Y=3 \% l’erreur est de 0.1 \mathrm{bp}.
On peut aussi tout simplement construire le « taux instantané » \text { y } défini par 1+y \cdot \Delta t=(1+Y)^{\Delta t}, mais cela complique le lien entre \text { y } et \text { Y }.
La formule ② donne la décomposition de la performance d’une obligation pendant un laps de temps, en un terme qui donne l’effet du temps et l’autre qui est dû au changement de niveau :
\text { perfTR = Investment Return en } \Delta t+\text { Speculative Return en } \Delta t
avec
\text { Investment Return en } \Delta t=\log (1+Y) ^{*} \Delta t
\text { Speculative Return en } \Delta t=-\operatorname{sensi} ^{*} \Delta Y
Pour avoir les indices Total Return, Investment Return et Speculative Return il suffit alors de les cumuler \text { indice Total Return de } t_{0} \text { à } t_{1}=100 * \text { produit cumulé des }(1+p e r f T R) \text { de } t_{0} \text { à } t_{1}
Idem pour obtenir les indices Investment Return et Speculative Return.
Mais dans la pratique de la gestion d’un portefeuille obligataire, le gestionnaire procède à des réinvestissements réguliers pour garder une duration voulue.
C’est la courbe des taux et son évolution qu’il suit. Si son portefeuille est par exemple centré autour du 10 ans, il regarde le niveau du 10 ans aujourd’hui, qu’il peut comparer à celui de hier ou d’il y a un an, et non le taux de tel ou tel titre qu’il a acheté il y a un certain temps.
Pour cette raison opérationnelle, ACE n’est pas appliqué à telle ou telle obligation, mais à des points de courbe.
ACE suit et analyse la performance des principaux points de courbe :
1an, 2ans, 5ans , 7ans, 10ans , 20ans, 30ans, sur les principales courbes d’Etat : US, Allemagne, France, UK, Japon.
ACE pour un point de courbe (constant maturity)
Exemple choisi
L’exemple choisi est le 10 ans allemand, obligation phare dans le marché de la zone Euro.
De nombreuses sources offrent des données riches sur les taux allemands depuis 35 années (mai 1997). Tous les jours ouvrés on a le taux du 10ans, et ceux du 7ans et 20ans permettent d’évaluer la pente de la courbe des taux, qui mesure la baisse du taux de l’obligation 10ans au cours du temps si la courbe est constante.
On peut représenter le suivi quotidien d’un 10 ans allemand comme si tous les jours on achetait une nouvelle obligation à 10 ans et qu’on vendait celle de la veille. En pratique l’Etat allemand émet une nouvelle 10 ans tous les 6 mois, et non tous les jours bien sûr.
Le 10 ans peut alors être répliqué avec un portefeuille constitué d’un titre de durée supérieure à 10 ans et d’un autre de durée inférieure, avec les pondérations adéquates, à adapter chaque jour.
On peut aussi traiter un Constant Maturity Swaps, exemple réel d’instrument à maturité fixée, comme si le roll était journalier.
Enfin il y a le future Bund 10 ans, le roll est trimestriel et la durée du future est à peu près constante. Mais les futures ont des spécificités techniques particulières, ils sont basés sur la livraison de titres appelés « cheapest to deliver » ; et la durée du Bund est plus proche de 9 ans que 10 ans.
Nous gardons l’exemple théorique d’un portefeuille rollé tous les jours, avec une obligation à 10 ans. Nous allons zoomer sur 7 années, pour une meilleure vision des performances, avec un cas particulier où on revient au point de départ.
La période choisie est du 10 juin 2015 au 22 avril 2022, parce que le 10 juin 2015 est le jour d’un pic du taux à presque 1%, après la remontée brutale au printemps 2015, et que le 22 avril 2022, le 10ans allemand a de nouveau affleuré 1%. Les valeurs exactes sont 0.981% et 0.963%, et nous avons forcé le taux du 22 avril 22 à 0.981%, à des fins démonstratives.
Ainsi un gérant qui par chance ou talent aurait acheté au plus haut du taux le 10 juin 2015, aurait été en plus-value pendant cette période de 7 années avant que la violente remontée de mars-avril 2022 ne l’annule.
Voir graphe (a)
Le taux du 10 ans ayant été longtemps négatif, sa moyenne est de 0.06%. Quelle est alors la performance réalisée de notre gérant ?
Elle va être présentée dans cette note avec son « Analyse en deux Composantes Exactes ».
Définition des « conditions inchangées »
pour un point de courbe
Le marché est inchangé est défini par « la courbe des taux est inchangée ».
Le Niveau du 10 ans est naturellement le taux actuariel du 10 ans, donné en input. Voir graphe (a)
Etape n°1 Combien cela rapporte de porter du 10 ans tous les jours ?
Porter du 10 ans en permanence rapporte plus que le taux actuariel du 10 ans, quand la courbe des taux est pentue. Le supplément de rendement, effet du rolldown, est égal au produit de la sensibilité par la pente.
Exemple : la pente est de 0.12% par an au niveau du 10 ans, soit 1 bp (0.01%) par mois. En supposant que la courbe des taux est la même en début et en fin de mois, le titre acheté il y a un mois n’a plus que 9 ans et 11 mois à vivre, donc son taux est 1 bp plus bas. Multiplié par la sensibilié de 10, cela fait un gain 0.10%, soit 1.2% par an. On a bien la formule
\text { Gain annualisé du rolldown }=\text { sensi } * \text { pente }=1.2 \% \text { dans l'exemple }
Faisons le calcul de la performance dans le cas général. Chaque jour l’obligation achetée va voir son taux varier
- i) parce que la courbe varie. Le mouvement de taux est noté Δtaux_{10 \text { ans }}
ii) et parce qu’elle descend dans la courbe. Ce mouvement est le rolldown.
Par définition de la pente, \text { rolldown }=\text { pente } ^{*}(-\Delta t)
(La durée du titre baisse de -\Delta t. Si la pente est positive, le taux baisse quand le temps s’écoule)
Le taux du titre va donc varier en sommant deux effets :
\Delta Y=\Delta \operatorname{tau} x_{10 a n s}+\text { rolldown }=\Delta t a u x_{10 a n s}-\text { pente }^{*} \Delta t ③
En reprenant la formule ②
\text { perfTR }=\log (1+Y)^{*} \Delta t-\operatorname{sensi} ^{*} \Delta Y
, la performance de l’obligation devient avec ③
\text { perfTR }=\log (1+Y)^{*} \Delta t-\operatorname{sensi} ^{*}(\Delta t a u x_{10 a n s}-\text { pente }^{*} \Delta t)
\text { perfTR }=(\log (1+Y)+ \operatorname{sensi} ^{*}\text { pente })^{*}\Delta t-\operatorname{sensi} ^{*}\Delta t a u x_{10 a n s} ④
Investment Return pendant \Delta t :
\text { R } * \Delta t effet du temp qui passe, avec
\text { R }=\log (1+Y)+ \operatorname{ sensi } ^{*}\text {pente }
R est le Rendement à courbe constante
Speculative Return pendant \Delta t :
effet de la variation de la courbe de taux
-\operatorname{sensi} ^{*}\Delta t a u x_{10 a n s}
\text {t a u x}_{10 a n s} est l’indicateur de Niveau

Le terme à multiplier \Delta t est le rendement ACE que nous cherchons.
Pour un point de courbe, on l’appelle le Rendement à courbe constante
R=\log (1+Y)+\text { sensi } ^{*} \text { pente } ⑤
La formule ④ devient
\operatorname{perfTR}=R^{*} \Delta t-\operatorname{sensi}^{*} \Delta \operatorname{taux}_{10 \mathrm{ans}} ④bis
Il faut bien noter que quand le titre a exactement 10 ans, on a en entrée son taux actuariel Y=\operatorname{taux}_{10 \mathrm{ans}}, mais le lendemain son \text {taux} Y n’est plus égal à \operatorname{taux}_{10 \mathrm{ans}}
Cela étant précisé, on peut itérer le calcul de R tous les jours de la série historique :
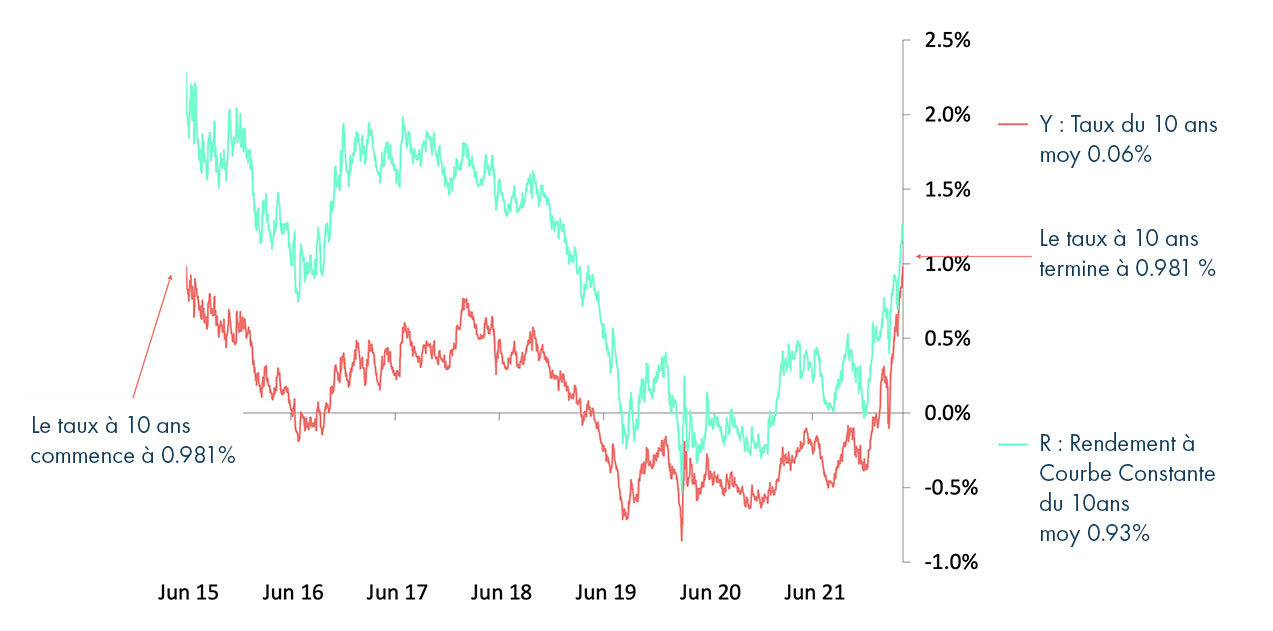
Graphe (a) Taux actuariel et Rendement à courbe constante du 10 ans allemand entre le 10 juin 2015 et le 22 avril 2022
La différence entre les deux courbes, égale au terme \text { sensi } ^{*} \text { pente } dépend du taux du 10 ans, mais aussi de la pente c’est-à-dire du taux de ses voisins. On constate que le Rendement à courbe constante est supérieur au taux actuariel ; cela vient du rolldown, la pente des taux ayant toujours été positive pendant cette période.
En moyenne le terme \text { sensi } ^{*} \text { pente } est de 0.93 \%-0.06 \%=0.87 \%
En simplifiant les valeurs et la formulation : la courbe des taux pentue permet d’obtenir un rapport de 1% avec un taux actuariel à 0%.
1.0 \%-0.06 \%=0.94 \%
Résumé de l’étape 1
La connaissance de la courbe des taux chaque jour donne pour chaque point de courbe (constant maturity) :
i) Son indicateur de niveau est par définition le taux puisqu’on a décidé que « marché inchangé » signifie « courbe des taux inchangée »
ii) Son Rendement « ACE » est le Rendement à courbe constante, obtenu par la formule ⑤
Etape n°2 Construction des indices Investment Return et Speculative Return
La formule ④ nous donne en lecture directe
\text { perfTR = Investment Return en } \Delta t+\text { Speculative Return en } \Delta t ④bis
avec
\text { Investment Return en } \Delta t=R * \Delta t
\text { Speculative Return en } \Delta t=-\operatorname{sensi}^{*} \Delta Y
Rappelons que le \text { taux Y } est donné en entrée et que le Rendement en courbe constante \text { R } est obtenu chaque jour avec les données de la courbe des taux.
En cumulant le produit des 1+R{ }^{*} \Delta t on obtient
l’Investment Return :
En cumulant le produit des 1-sensi{ }^{*} \Delta Y on obtient
le Speculative Return :
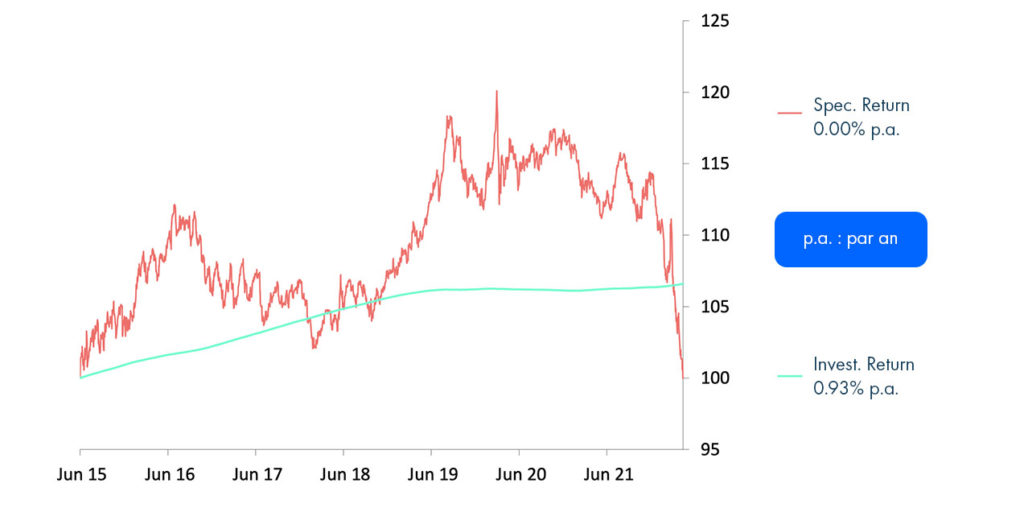
Commentaires sur le Speculative Return
Le Speculative Return est obtenu de jour en jour en cumulant les 1-sensi{ }^{*} \Delta Y en ayant bien calculé la sensibilité, de sorte qu’il n’y a pas d’approximation linéaire. Après 6503 jours ouvrés, le Speculative Return, retombe sur 100, comme au point de départ le 10 juin 2015 , ce qui nous convient bien étant donné que le taux du 10 ans est revenu exactement à 0.981% comme au départ.
Précision : pour revenir à exactement 100, il a fallu un traitement d’un effet de convexité, qui perturbe les calculs de 0.07% par an. Ce point technique est traité en Annexe.
Commentaires sur le Investment Return
Par nature, la volatilité de la performance est logée dans le Speculative Return et non dans l’Investment Return, obtenu de jour en jour en cumulant les facteurs 1+R{ }^{*} \Delta t
Nous pouvons observer à quel point l’Investment Return trace une courbe régulière, avec une « vitesse » maitrisable.
Nous distinguons bien les périodes où l’indice Investment Return croit vite, et celles où il stagne.
Pourtant nous sommes partis du Rendement à Courbe Constante bien bruité, tel qu’il apparait dans le graphe (a).
Ceci est vrai pour les obligations comme ce le sera pour les actions : ils ont aussi un taux d’Investment Return qui peut vibrer, mais le cumul de ce taux multiplié par \Delta t est très régulier.
Retenons cette image : les actifs seraient comme des voitures à carburateurs mal réglés, avec un compteur de vitesse qui vibre, mais ayant une allure régulière aux yeux d’observateurs extérieurs.
Etape n°3 Vérification du Total Return
Chaque jour, avec la connaissance de la courbe on induit le taux actuariel du titre acheté la veille, qui a comme durée 10 ans – 1 jour, et qu’il faut revendre, en même temps que le nouveau 10 ans est acheté. En calculant sa valeur actuarielle on a la performance du jour.
La question est : retrouve-t-on par ce calcul direct la même performance TR quotidienne que celle obtenue par la formule ④ ou ④bis , en sommant le Speculative Return et l’Investment Return obtenus par des autres méthodes ?
La réponse est positive, au dixième de bp près. Les mathématiques l’avaient prévu mais il y a une série de barrières techniques à franchir et c’est une vérification de l’exactitude des méthodes de ACE.
Les résultats sont résumés dans le graphe (b) :
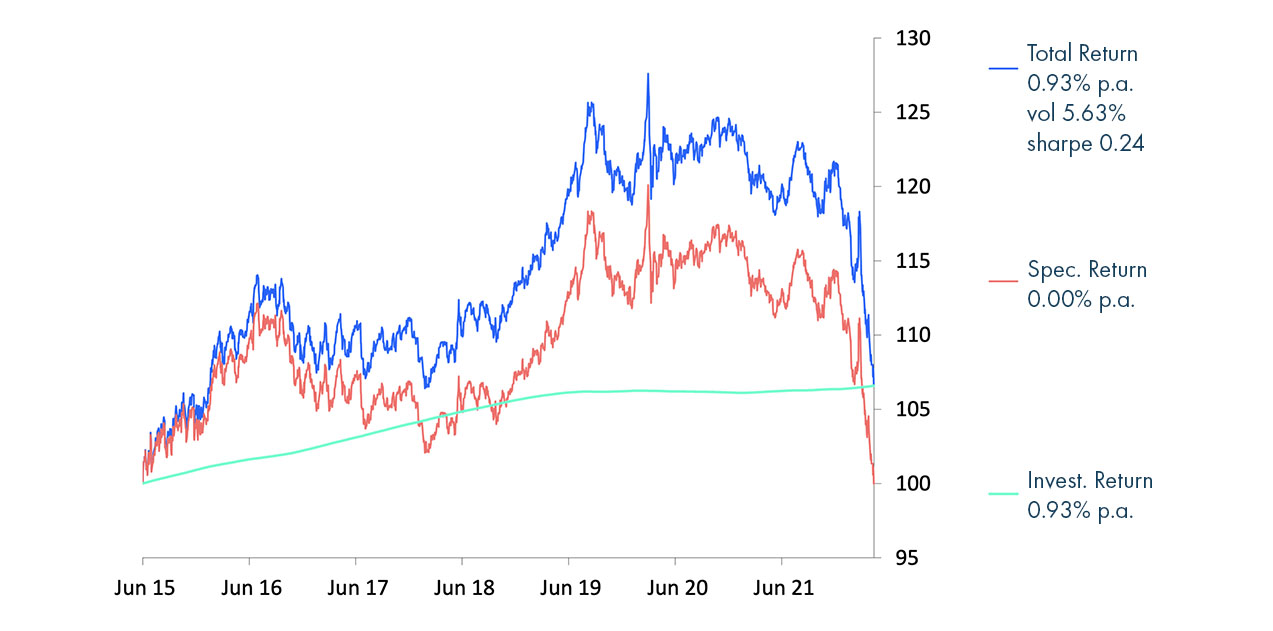
Graphe (b) Décomposition par ACE de la performance Total Return du 10 ans allemand entre le 10 juin 2015 et le 22 avril 2022
Résumé des étapes 2 et 3.
En cumulant resp. l’effet de la variation du Taux à 10 ans et l’effet du Rendement à courbe constante avec le temps, on obtient resp. le Speculative Return et l’Investment Return.
La somme des deux termes redonne la performance Total Return au dixième de bp près.
Retenir que l’Investment Return est très régulier alors que le Rendement est bruité.
Etape n°4 Décomposition de la performance Excess Return
On préfère souvent mesurer la performance au monétaire.
L’Excess Return est défini chaque jour par:
\text { Excess Return en } \Delta t=\text{Total Return en } \Delta t-refi^{*}\Delta t
avec \text { refi } le refinancement du titre.
Par abus de notation on écrit pour les indices \text { Excess Return } =\text{ Total Return } – \text { refi }
et on définit le Net Investment Return :
\text { Net Investment Return } =\text{ Investment Return } – \text { refi }
Le Speculative Return est inchangé qu’on raisonne en Total Return ou en Excess Return, car il n’a pas d’autre mission que de suivre le niveau de valorisation, insensible à l’effet du temps qui passe.
Ayant ôté le refi du Total Return et de l’Investment Return on obtient la décomposition par ACE de la performance Excess Return.
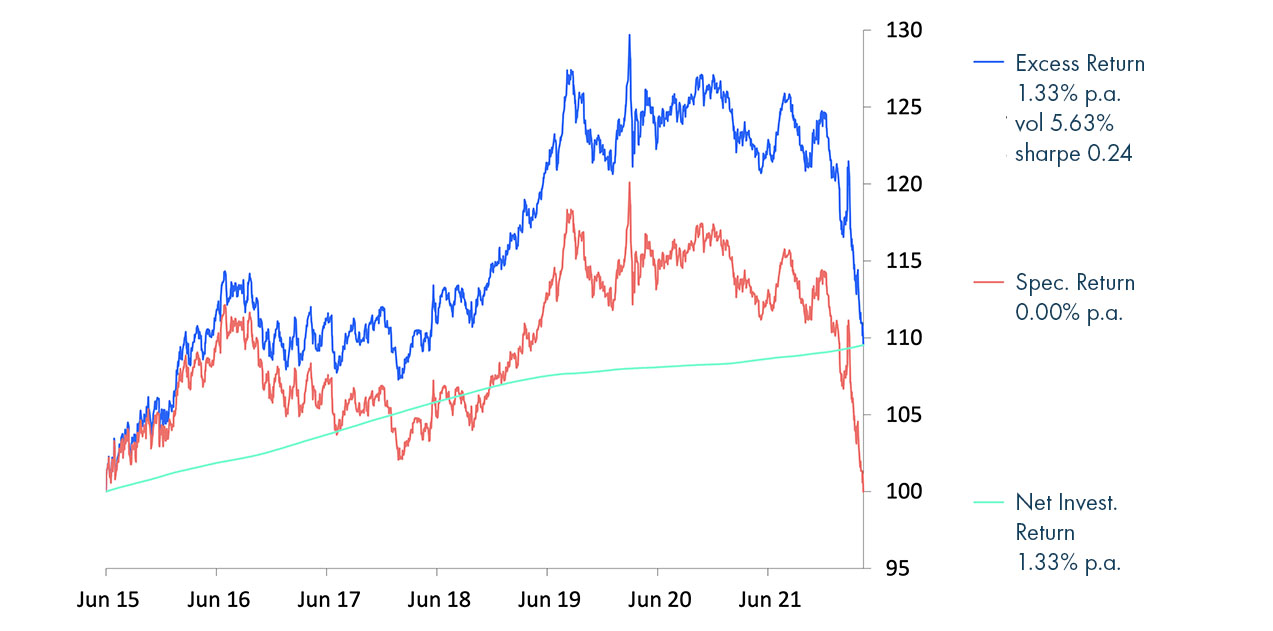
Graphe (c) Décomposition par ACE de la performance Excess Return du 10 ans allemand entre le 10 juin 2015 et le 22 avril 2022
Dans le cas particulier du 10 ans allemand de juin 2015 à avril 2022 le refinancement a été négatif, d’où une performance Excess Return supérieure à celle du Total Return.
Résumé des étapes 4.
En reprenant termes du cahier des charges de ACE :
Pour un point de courbe (constant maturity)
i) le rendement ACE à conditions inchangées du point de courbe est le Rendement à courbe constante : taux actuariel + effet du roll-down
ii) le niveau de valorisation du point de courbe est défini par son taux actuariel.
ACE découpe la performance Total Return du point de courbe en deux termes :
iii) la courbe « Invest return » qui est le cumul de jour en jour du Rendement à courbe constante
iv) la courbe « Speculative return » est le cumul de l’effet des variations du taux du point de courbe
Si le taux à l’arrivée est le même que le taux au départ pendant une période donnée, que ce soit un jour, ou plusieurs années, le Speculative return a une performance annualisée de et la performance est égale à l’Investment Return, comme on le voit dans les graphes (a) et (b).
ANNEXE sur l’effet de convexité
Les effets dits de convexité sont des sources de malentendus, d’erreurs parfois.
Il est nécessaire ici de le mentionner car il a fallu le prendre en compte pour que l’indice Spec. Return revienne à 100, quand le taux revient au même niveau qu’au départ. Comme dit Riccardo Rebonato, la convexité d’une obligation n’est pas une source de performance pour celui qui porte la porte de manière passive.

Mais pour maintenir un portefeuille de maturité constante de 10 ans, il faut faire des transactions – roller du 10 ans tous les jours dans cet exemple, et ces ajustements sont source potentielle de performances.
Nous avons résolu l’effet de convexité avec une formule explicite, dépendant des caractéristiques du 10 ans et de la volatilité de son taux. Dans le cas du 10 ans allemand de juin 2015 à avril 2022, cela donne un effet négatif de -0.07% par an.
La vérification annoncée à l’étape 3 est avérée, convexité ou non :
\text { perfTR = Investment Return en } \Delta t+\text { Speculative Return en } \Delta t
avec
\text { Investment Return en } \Delta t=\log (1+Y)^{*} \Delta t
\text { Speculative Return en } \Delta t=-sensi{ }^{*} \Delta Y
Nous avons pris la décision d’ôter l’effet convexité au Speculative Return et de l’ajouter à l’Investment Return :
\text { Speculative Return en } \Delta t=-sensi{ }^{*} \Delta Y-\text { effet convexité en }\Delta t
\text { Investment Return en } \Delta t=-sensi{ }^{*} \Delta Y+\text { effet convexité en }\Delta t
, au motif que le Speculative Return doit être un indicateur de niveau, ne dépendant pas du chemin suivi entre le taux de départ et le taux d’arrivée ; qu’au contraire un effet de convexité peut être rangé dans la catégorie « effet du temps qui passe »
L’idée fonctionne car compte tenu de ces corrections (de -0.07% par an) nous obtenons les résultats du graphe (b) :
L’Invest. Return va de 100 à 106.57, avec une performance annualisée de 0.93%.
Le Spec. Return entre le 10 juin 2015 et le 22 avril 2022 va de 100 à 100 , sa performance est nulle. C’est le résultat espéré, le Speculative Return ainsi construit est bien un indice de niveau compatible avec le taux actuariel, qui vaut au départ et à l’arrivée 0.981%.
Le Total Return va de 100 à 106.57, comme l’Investment Return.